ANIMATIONS

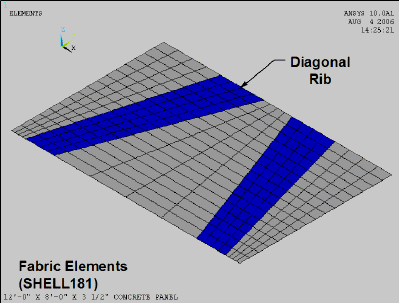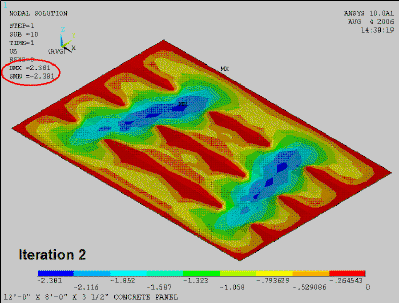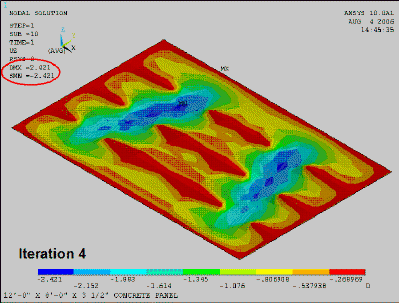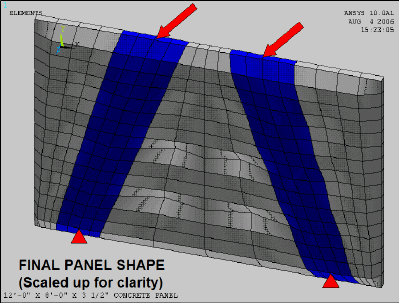
<align justify>This animation shows a fabric-formed panel going through temperature changes during the initial curing cycle due to the heat of hydration. Geotextile fabrics are temperature sensitive, and as a result, creep as the temperature increases. Creep may be more of a factor as the concrete panel cures due to the heat of hydration than initially as the concrete is being poured into the fabric formwork.</align>

<align justify>This animation shows a fabric-formed concrete panel going through the form-finding process using ANSYS. While not as accurate as using ADINA in combination with an EXCEL spreadsheet it none-the-less shows an automatic process using an ANSYS script.</align>

<align justify>This animation shows a fabric-formed panel undergoing cyclic loading due to positive and negative wind loads. This FEA model uses only plain concrete, no reinforcing, thus the governing criterion for structural plain concrete design is the uniaxial cut off strength of the concrete or Modulus of Rupture. Maximum principal tensile stresses resulting from positive and negative wind loads combined with gravity loads must fall below this value, which for 5,000 psi concrete is 353.6 psi. When the maximum principal tensile stress is greater than the Modulus of Rupture, the ADINA model indicates this point by a “crack” in the panel model (red circles). The ADINA Theory and Modeling Guide notes: “…for concrete…. these are true principal stresses only before cracking has occurred. After cracking, the directions are fixed corresponding to the crack directions and these variables are no longer principal stresses”. ADINA uses a “smeared crack” approach to model the concrete failure.</align>

<align justify>It may be observed that under the positive lateral load case the panel does not crack, within the body of the panel, as the load is incrementally increased from 1.4 to 1.8 times the factored positive load. However, under the factored negative lateral load case, the panel shows progressively more cracks as the load is increased. </align>